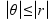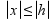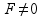Eksperimentalni rezultati
Uz ovaj rad, NEAT tehnika je implementirana na par problema. Prvo, standardni problemi treniranja mreža koje rešavaju eksluzivno ili (xor) i problem balansiranja inverznog klatna na kolicima (pole balancing problem). Zatim, NEAT je korišćen da trenira botove za igricu Racer, u kojoj oni treba da kontrolišu pojednostavljena kola u trci.
Eksluzivno ili
Eksluzivno ili je logička operacija koja ima dva ulaza i jedan izlaz. Svaki ulaz može imati vrednost tačno (1) ili netačno (0). Izlaz je tačan kada su ulazi različiti, netačan inače.
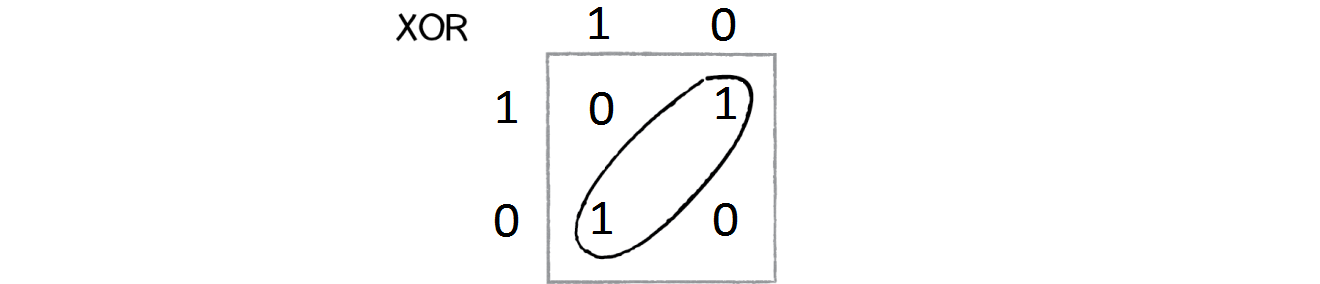
Ovaj problem je zanimljiv jer nije linearan, i samim tim nemoguće je rešiti ga bez skrivenih neurona u mreži. Time možemo da testiramo da li NEAT radi i da li se skriveni neuroni stvaraju vremenom.
Mreže su trenutne. Izlaz mreže je relan broj između 0 i 1, interpretiran kao netačno (0) ako je izlaz manji od 0.5 i tačno (1) inače. Svaka mreža se testira na sva četiri logička slučaja za eksluzivno ili. Prilagođeonst mreže se računa kao:
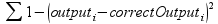
Dakle, maksimalan fitnes je 4. Fitnes sa kojim smo zadovoljni (tad prekidamo treniranje) je postavljen na 3.9.
Prva mreža koja daje tačne odgovore dobijena je u 14. generaciji. U 94. generaciji postignut je fitnes 3.9. Prva mreža koja je postigla taj fitnes izgleda ovako:
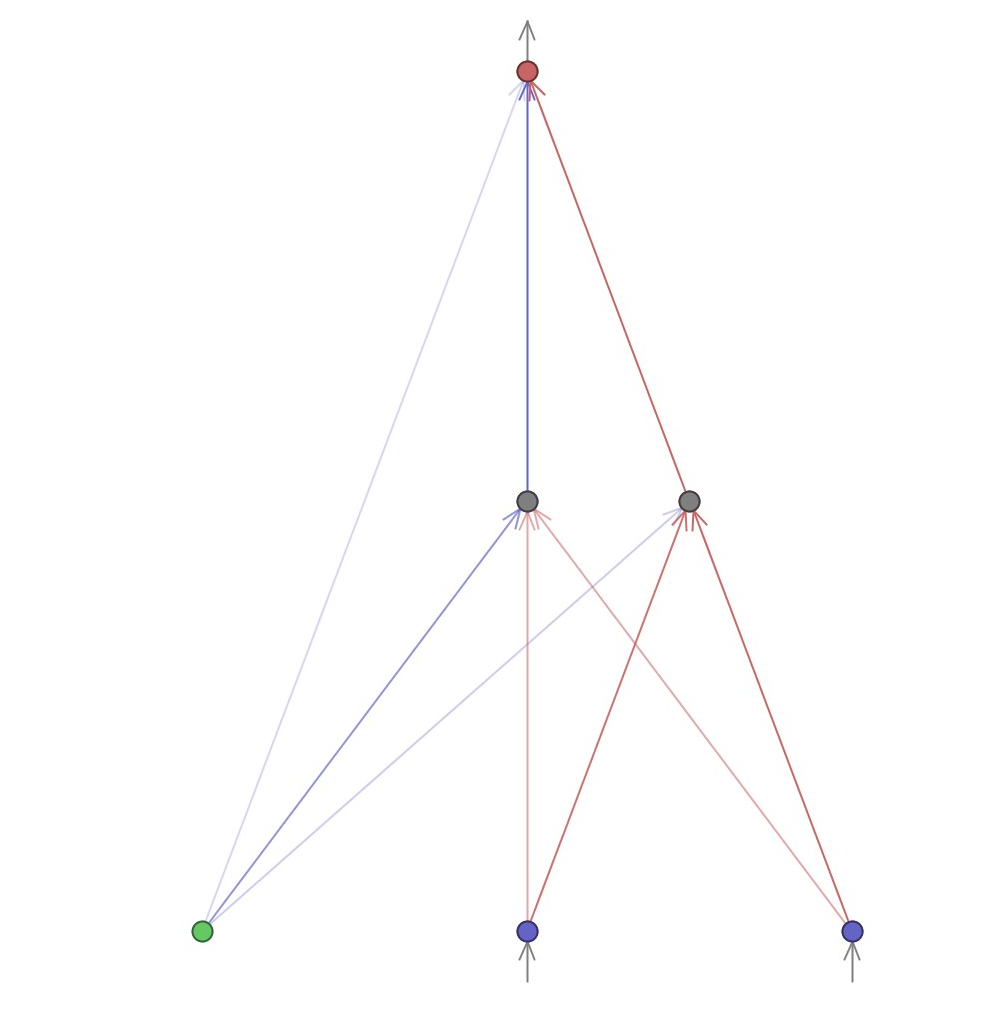
Ovo je u isto vreme i najmanja moguća mreža koja rešava problem. Zatim je eksperiment ponovljen 100 puta. 16 puta mreža nije uspela da se istrenira u 1000 generacija. U ostalim slučajevima, ovo su podaci:
| min | prosek | maks | |
| generacija | 71 | 104,3 | 322 |
| broj neurona | 6 | 6,75 | 16 |
| broj veza | 9 | 11,65 | 37 |
Dakle, naša implementacija NEAT-a je uspešno i dosta minimalno rešila ovaj problem. Možemo da pređemo na problem balansiranja šiške na kolicima.
Balansiranje inverznog klatna na kolicima
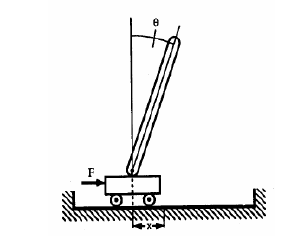
Na šinama postoje kolica na kojima postoji inverzno klatno. Ovaj problem zahteva dizajniranje kontrolera koji u svakom trenutku utiče silom na kolica po x osi, tako da kolica ostanu na šinama i da ugao klatna ostane u zadatom ugaonom intervalu. Ulaz je definisan sa četiri realne vrednosti: ugao klatna  , ugaona brzina klatna
, ugaona brzina klatna 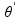 , pozicija kolica relativna na sredinu šina
, pozicija kolica relativna na sredinu šina 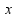 i brzina kolica
i brzina kolica 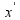 . Izlaz sistema je sila
. Izlaz sistema je sila 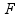 iskorišćena u datom trenutku. Stanje sistema se opisuje sledećim parametrima:
iskorišćena u datom trenutku. Stanje sistema se opisuje sledećim parametrima:
| simbol | ime | objašnjenje |
 |
ugao klatna | 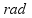 |
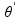 |
ugaona brzina klatna | 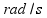 |
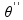 |
ugaono ubrzanje klatna | 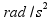 |
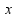 |
pozicija kolica | udaljenost od sredine šina, 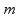
|
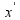 |
brzina kolica | 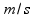 |
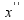 |
ubrzanje kolica | 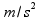 |
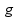 |
gravitaciono ubrzanje | 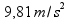 |
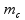 |
masa kolica | 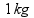 |
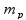 |
masa klatna | 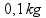 |
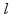 |
dužina klatna | dužina do sredine klatna, 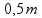
|
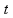 |
vreme | 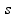 |
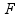 |
sila | sila kojom sistem utiče na kolica u nekom trenutku, 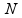
|
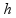 |
limit šina |
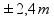 od centra šina od centra šina |
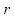 |
limit ugla klatna |
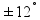 od od 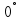
|
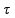 |
vremenski korak | korak korišćen u simulaciji, 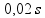
|
Pretpostavke radi pojednostavljenja simulacije:
- trenje se igoniriše
- odgovor sistema je trenutan
- točkovi ne klizaju
- ne postoji granica momenta sile
Važe sledeće jednačine kretanja:
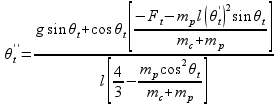
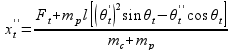
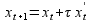
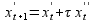
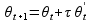
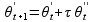
Ograničenja u svakom trenutku simulacije:
Kada se neko od ovih ograničenja naruši simulacija se završava. Ako se simulacija završi posle vremena 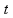 , funkcija prilagođenja data je sa
, funkcija prilagođenja data je sa 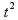 . Mreža je istrenirana kada izdrži 10000 sekundi simulacije.
. Mreža je istrenirana kada izdrži 10000 sekundi simulacije.
Ulaz je definisan sa četiri realne vrednosti: ugao klatna  , ugaona brzina klatna
, ugaona brzina klatna 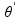 , pozicija kolica relativna na centar šina
, pozicija kolica relativna na centar šina 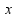 i brzina kolica
i brzina kolica 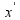 . Ispostavlja se da je ovaj problem linearan. Rešava ga nasumična mreža iz inicijalne populacije:
. Ispostavlja se da je ovaj problem linearan. Rešava ga nasumična mreža iz inicijalne populacije:
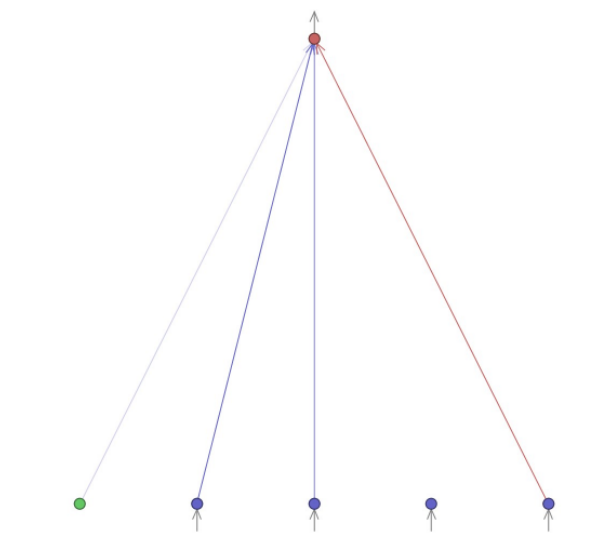
Zakomplikujmo malo problem, umesto četiri ulaza ( ,
, 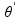 ,
, 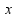 i
i 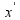 ), dajmo mreži samo dva ulaza (
), dajmo mreži samo dva ulaza ( ,
, 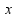 ). Da bi mreža rešila ovaj problem, mora sama izračunati izvod, tj. koristiti informacije od prethodnog poziva mreže. Dakle, treba nam trenutna mreža. Skalirajmo oba ulaza na broj između 0 i 1 pre nego što ih pošaljemo kao ulaz.
). Da bi mreža rešila ovaj problem, mora sama izračunati izvod, tj. koristiti informacije od prethodnog poziva mreže. Dakle, treba nam trenutna mreža. Skalirajmo oba ulaza na broj između 0 i 1 pre nego što ih pošaljemo kao ulaz.
Naša implementacija NEAT-a uspešno je rešila i ovaj problem. Prvi put je mreža prešla 10000 sekundi u 19. generaciji. Ta mreža izgleda ovako:
Na slici se ne vidi dobro, ali postoji povratna veza od izlaznog neurona ka skrivenom neuronu. Ta veza omogućava da ulazni podaci budu ne samo pozicija kolica i ugao klatna, već i zadnja iskorišćena sila.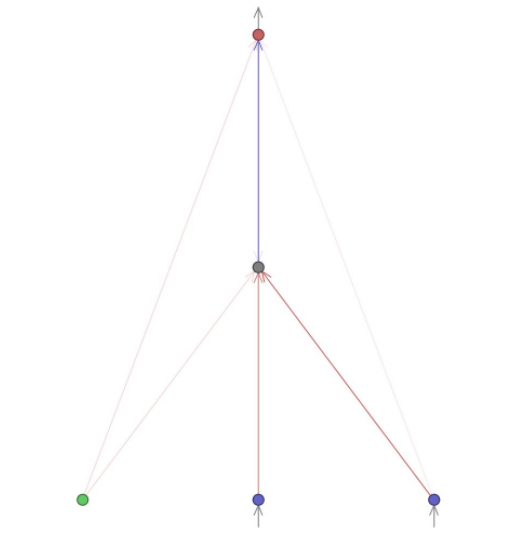
Test je ponovljen 100 puta. Od tog broja 25 puta mreža nije uspela da se istrenira za 1000 generacija. U ostalim slučajevima, ovo su podaci:
| min | prosek | maks | |
| generacija | 7 | 104,84 | 925 |
| broj neurona | 5 | 5,61 | 11 |
| broj veza | 6 | 7,71 | 22 |
Dakle, NEAT je rešio i ovaj problem formirajući mrežu koja u većini slučajeva ima minimalan broj neurona. Pređimo na igricu Racer.
Racer
Racer je jednostavna trkačka igra u kojoj igrač kontroliše svoje vozilo. Cilj je da se za dato vreme pređe što veći put. Igrač bira potez 60 puta u sekundi. Potez može sadržati skretanje u levo za mali ugao, skretanje u desno, kretanje napred i kretanje nazad, tj. bilo kakvu kombinaciju tih aktivnosti. Ako vozilo udari u ivicu mape brzina mu se spušta na nulu. U svakom trenutku poznata je udaljenost do koje je igrač stigao. Aplikacija je priložena uz diplomski, može da se igra, da se kreira mapa, da se trenira NEAT bot za igricu i da se prati proces treniranja.
Proces treniranja u aplikaciji može da se prati kroz praćenje funkcije prilagođenja kroz generacije, udaljenosti kroz generacije, broja neurona kroz generacije, broj veza kroz generacije i vrsta kroz generacije. Takođe, može da se uđe u svaku generaciju i pogleda statistika i kako je igralo 5 najboljih botova, zatim u svaku vrstu u generaciji i pogleda statistika i igru najboljih 5 botova, zatim u jedinku i da se vidi njena mreža i da se igra protiv nje.
Sada da vidimo kako da spremimo ulaz za mrežu. U svakom trenutku igre program zna najbližu tačku od igrača na liniji koja prolazi sredinom staze. Za svaku tačku sredine puta zna koliko je udaljena od početka kruga. Uzmu se tačke za 100, 200 i 300 udaljene od igrača na sredini staze. Od svake od njih nađe se ugao i udaljenost od trenutne pozicije igrača, i doda se dodatna tačka koja je ugao i jačina trenutnog vektora brzine vozila. Od uglova se oduzme ugao igrača (smer u kojem je vozilo okrenuto), da bi se dobio relativan ugao u odnosu na trenutno stanje vozila, i sve te vrednosti se skaliraju na vrednosti između -1 i 1 (uglovi se podele sa pi, udaljenosti se podele sa 100, 200, 300 i 5 – maksimalna jačina vektora brzine). Ovih 8 vrednosti koriste se kao ulaz u mrežu. Postoje četiri izlaza, po jedan za svaku moguću aktivnost (levo desno gore dole).
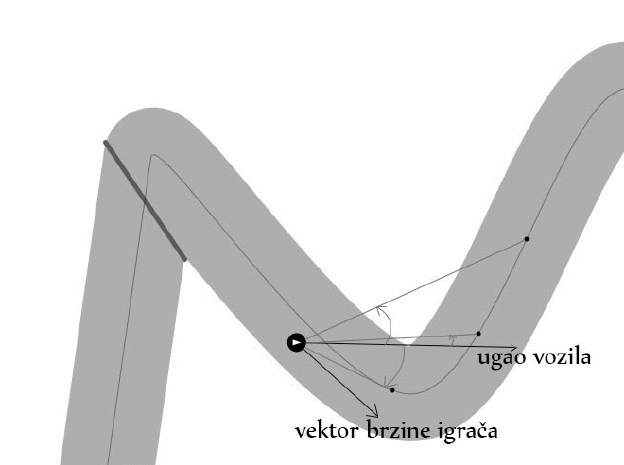
Svakom botu je dato da igra simuliranih 30 sekunda igrice. Posle toga, gleda se koliko je prešao svaki bot (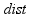 ). Funkcija prilagođena data je kao
). Funkcija prilagođena data je kao 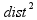 . Korišćena je trenutna mreža.
. Korišćena je trenutna mreža.
NEAT je uspeo da reši i ovaj problem, tako da botovi igraju na nivou čoveka (dobro izvežbani čovek može da pobedi bota).
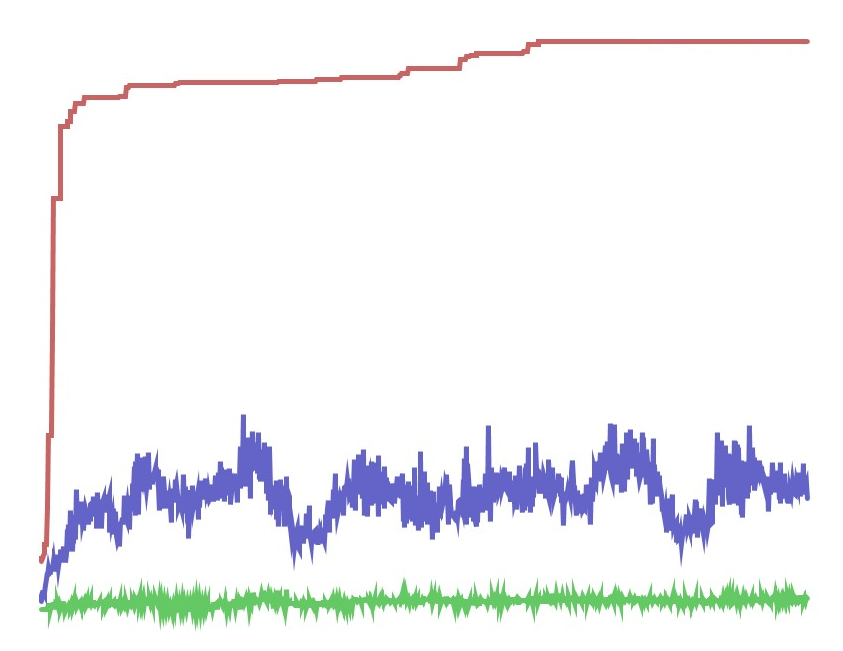
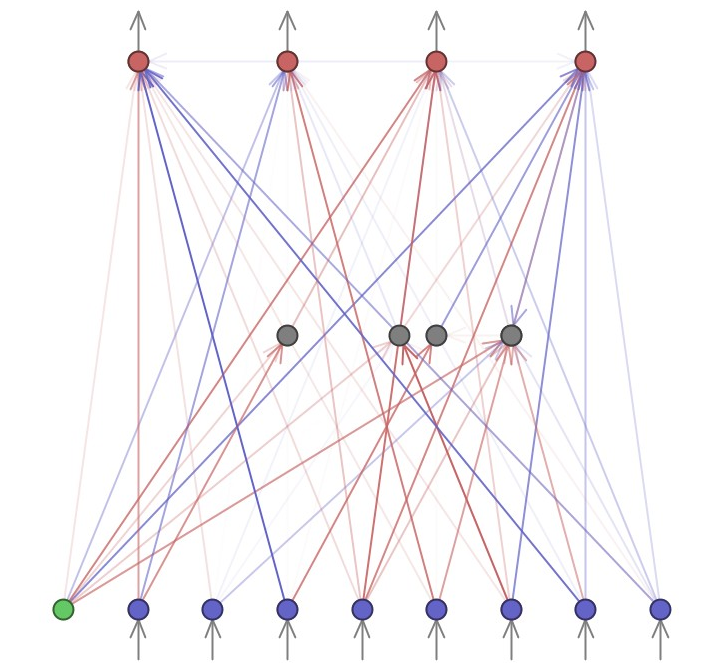
Zaključak
Neuralne mreže su neizbežne za rešavanje raznih problema. U određenim slučajevima postoje dobro poznati algoritmi za njihovo treniranje, i tada ih treba koristiti. Međutim, u slučajevima u kojim nije tako lako iskoristiti konvencionalne metode za treniranje mreže, može se razmišljati o NEAT rešenju.
Opisana implementacija ove tehnike (prema receptu njenih izumitelja) je naletela na nekoliko zidova o kojima treba razmišljati. Dodavanje novih neurona nije laka operacija, često pri samoj mutaciji dodavanja jedinka izumre zbog loše prilagođenosti, i kada se doda potrebno je dosta generacija da se taj neuron poveže sa drugim neuronima. Kada se dodaju nove veze njihove težine se inicijalizuju na neke male nasumične vrednosti, i samim tim potencijalno ostaju nevažne u odnosu na veze koje već duže postoje u sistemu i mutacijom su dosta otežale. Takođe, puno rada treba provesti u finom podešavanju vrsta, njihovih razlika, broja i bonusa i penala koje donose.
Sa druge strane, čak i sa tim problemima ova implementacija uspela je da reši klasične benčmark probleme za slične tehnike, pa čak i dosta dobro da vozi kola (u igrici). Takođe, pokazalo se da dosta dobro i minimalno rešava probleme u kojima ima malo ulaza, izlaza, i koji zahtevaju malo skrivenih neurona.
NEAT je tehnika u povoju, i postoji svega 10-ak godina. Nije savršena, ali se potencijalno može unaprediti u budućnosti. To je tema koja zahteva dodatna istraživanja.